─ 4象限マトリクス・Φの式・効果量・分散の影響まで一望で理解 ─
✍️ はじめに
仮説検定の学習をしていて、
- 「第1種の過誤と第2種の過誤の定義があいまいになる」
- 「偽陽性と偽陰性がどちらか分からなくなる」
- 「αと1−β、どっちが検出力?」
といった混乱に陥った経験はありませんか?
これらが頭の中でグチャグチャに絡み合い、ゲシュタルト崩壊寸前になりそうな人へ、構造的な整理法と、解法に必要な4象限の視点をご紹介します。
🧭 仮説検定の4象限マトリクス+Φによる数式表現
想定:検定統計量 $ X \sim N(\theta, 1) $、棄却域 $ X \geq x_0 $
| 実際\判定 | H₀が真 | H₁が真 |
| 陰性(棄却しなかった) | ✅ 真陰性 $ 1 – \alpha(x_0) = \Phi(x_0) $ 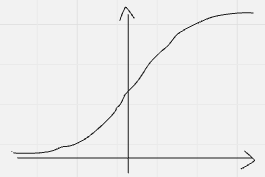 | ❌ 偽陰性(第2種の過誤) $ \beta(x_0) = \Phi(x_0 – \delta) $ 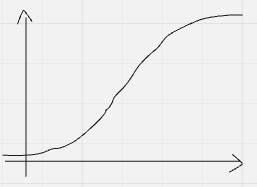 |
| 陽性(棄却した) | ❌ 偽陽性(第1種の過誤) $ \alpha(x_0) = 1 – \Phi(x_0) $  | ✅ 真陽性(検出力) $ 1 – \beta(x_0) = 1 – \Phi(x_0 – \delta) $  |
🔄 効果量 $ \delta $ が変わるとどうなるか?
- $ H_1: \theta = 1 $ → $ 1 – \Phi(x_0 – 1) $
- $ H_1: \theta = 2 $ → $ 1 – \Phi(x_0 – 2) $
- $ H_1: \theta = 3 $ → $ 1 – \Phi(x_0 – 3) $
$ \delta $ が大きいほど $ x_0 – \delta $ は小さくなり、$ \Phi $ の値(=β)は小さくなる → 検出力 $ 1 – \beta $ は大きくなる
🧮 分散($ \sigma^2 $)が変わるとどうなるか?
1. 第1種の過誤 α:
$$\alpha = 1 – \Phi\left( \frac{x_0}{\sigma} \right)$$
$ \sigma $(標準偏差)が大きいと $ \frac{x_0}{\sigma} $ は小さくなり → $ \Phi $ の値は小 → αは大きくなる
2. 第2種の過誤 β:
$$\beta = \Phi\left( \frac{x_0 – \delta}{\sigma} \right)$$
$ \sigma $ が大きいと $ \Phi $ の引数が小さくなり → βが大きくなる → 検出力($ 1 – \beta $)は小さくなる
✅ 分散と検出力の関係まとめ
| 分散($ \sigma^2 $) | $ \alpha(x_0) = 1 – \Phi\left( \frac{x_0 – \mu_0}{\sigma} \right) $ | $ \beta(x_0) = \Phi\left( \frac{x_0 – \mu_1}{\sigma} \right) $ | 検出力$ 1 – \beta(x_0) = 1 – \Phi\left( \frac{x_0 – \mu_1}{\sigma} \right) $ |
| 小さい | 小さい | 小さい | 大きい |
| 大きい | 大きい | 大きい | 小さい |
📎 定型の数式テンプレート(片側検定)
$$ \alpha(x_0) = 1 – \Phi\left( \frac{x_0 – \mu_0}{\sigma} \right) $$
$$ \beta(x_0) = \Phi\left( \frac{x_0 – \mu_1}{\sigma} \right) $$
$$ 1 – \beta(x_0) = 1 – \Phi\left( \frac{x_0 – \mu_1}{\sigma} \right) $$
- $\mu_0$:H₀の平均
- $\mu_1 = \delta$:H₁の平均
- $\sigma$:標準偏差(√分散)
この4象限とΦの式を使えば、仮説検定の混乱を整理しやすくなります。